If you work in industrial engineering, you’ve likely heard about the various construction cost estimate classes and their ranges of accuracy.
This article explains how project cost estimates are generated and the differences between the classes.
Professional Estimating
As a design project progresses, it’s common for project management teams to produce multiple estimates during the preliminary design, detailed engineering, and tendering phases.
The completed project estimates become more accurate as the project’s level of definition increases.
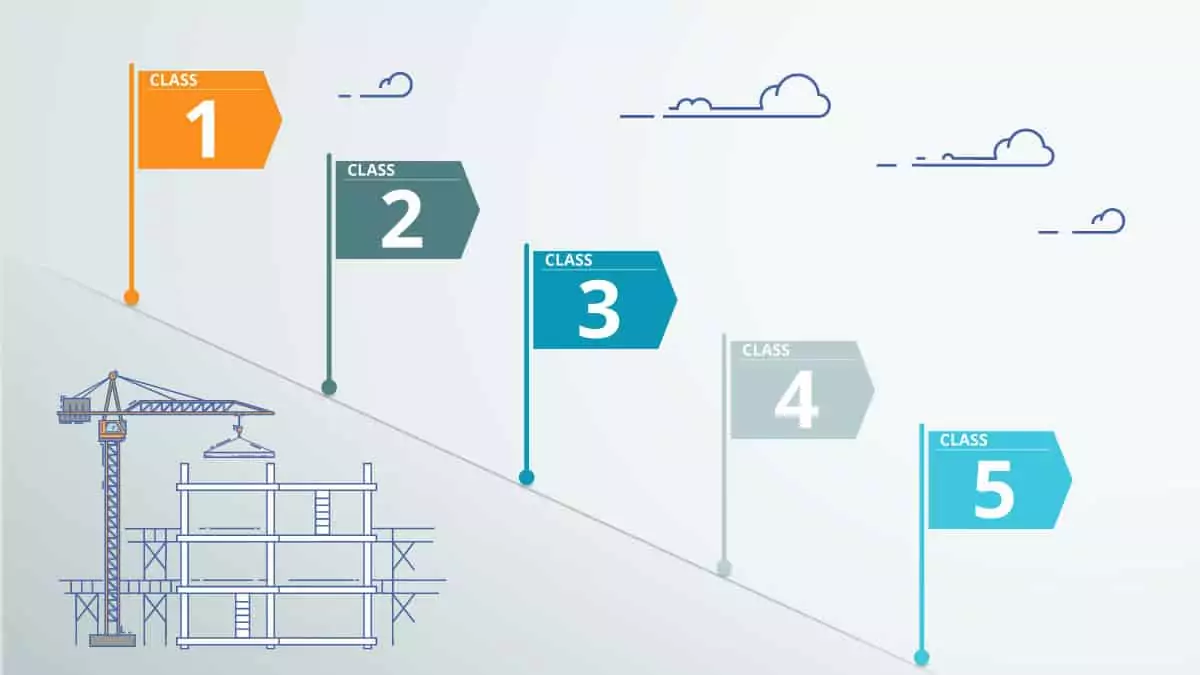
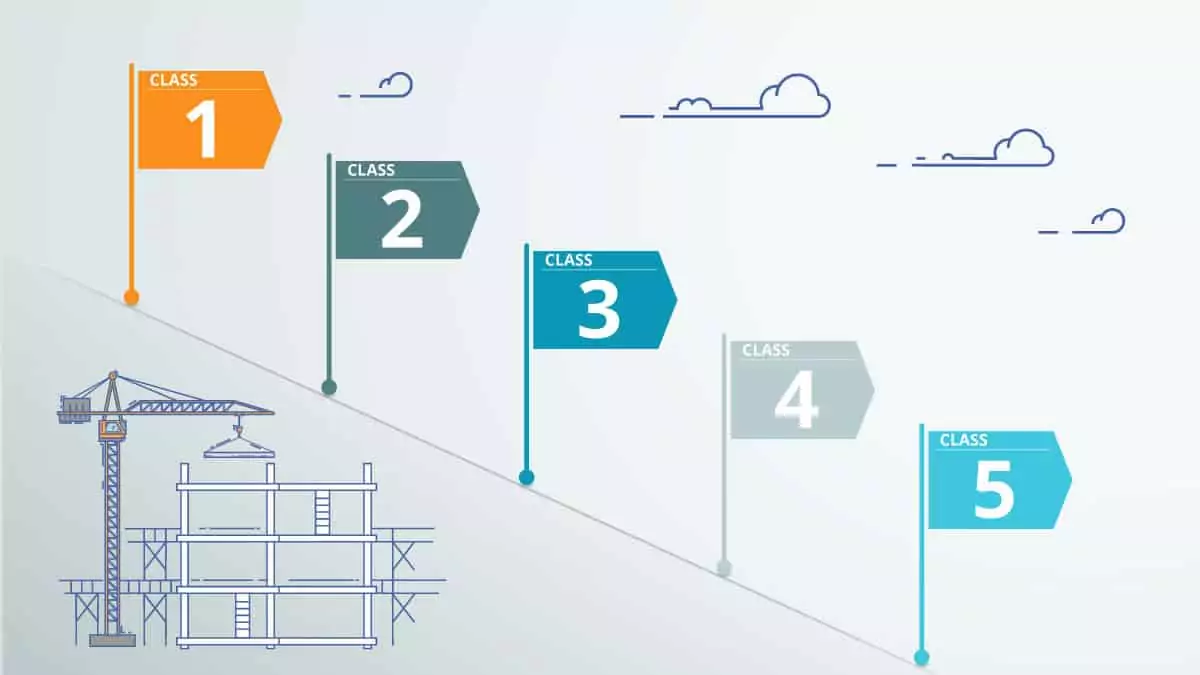
Professional organizations around the world, such as AACE International, established global practices for cost estimation. They use a five-level system of cost estimate classifications. Going up the hierarchy, the classes of estimates become increasingly more detailed and reliable.
Of course, each class also requires more effort and more completed deliverables.
To produce an accurate estimate, the project team will likely use at least some of the following tools and inputs:
- A historical cost database and unit prices
- An estimation software
- Stick estimating
- Market trends
- Labor costs
Typical construction projects use these inputs to generate thousands of line items. Preparing detailed estimates takes hundreds of hours to complete and includes gathering project data and completing engineering.
Traditional vs. Rapid Cost Estimating
In traditional project execution models, it’s practically impossible to jump straight to higher estimate levels without putting in the work.
At Vista, we’ve developed a rapid construction cost estimating technique that leverages the digital tools we use to improve project execution efficiency in our engineering services.
Construction Cost Estimate Classes
Class 5
This is known as the rough order of magnitude (ROM) estimate.
It is used for the initial screening projects for capital expenditure planning. Since several projects are initially available, estimating each would require a tremendous amount of time and effort. Given the limited preparation, ballpark figures are usually accepted to make business plan projections.
Class 5 estimates are drawn from inadequate information which is about 0 to 2% of the project definition.
The information may be nothing more than a basic description of the plant or process, capacity, and location. That is why its accuracy ranges -50% on the low side and +100% on the high side.

Stochastic cost estimating methods are used for obtaining a Class 5 estimate. Examples of these are cost/capacity curves, rule of six-tenths, Lang factor method, scale of operation factors, and cost indices. These techniques use parametric cost estimation methods to deduce the total cost of a given project.
Class 4
A Class 4 estimate is considered a feasibility study estimate. It is used by organization heads and construction managers for strategic business planning. A more detailed approach is required since this will determine the viability of the project. Moreover, alternative project schemes are evaluated for their economic value.
Feasibility studies for industrial constructions often require the definition of roughly around 1 to 15% of the project. Aside from basic descriptions, other inputs that influence project costs include:
- process flow diagrams (PFDs)
- major construction activities
- equipment lists

This brings an estimated accuracy of -15 to -30% and +20 to +50% on the low and high sides, respectively.
The cost estimation methods used for achieving a Class 4 estimate are virtually the same as those used in Class 5. However, factoring and proportioning are used on more specific items. An example is estimating the cost of a processing unit, which is only a part of the total capital cost.
Class 3
In project management, this is the first control estimate and takes place at the beginning of the project planning stage.
It is distinct from the first two classes which are prepared in the project initiation stage. The Class 3 estimate is the actual capital an organization allocates for a specific project. Hence, it is often termed as the budgetary estimate.
A Class 3 estimate is developed from a preliminary or basic engineering design (BED). The engineering phase of the project is 10% to 40% completed. An overview of the project scope is available along with the expected timeline.

Preliminary references are also established for bidding. Examples of these include:
- plot plans
- general assembly drawings
- piping and instrument diagrams (P&ID)
- utility diagrams
- equipment lists
- general standards
- specifications
Detailed equipment specifications for critical equipment are included as well. Usually, these have the most significant impact on the total project cost.
Given the level of detail of Class 3 estimates, its accuracy ranges from -10 to -20% on the low side and +10 to 30% on the high side.
Class 2
A Class 2 estimate is known as the bid or tender estimate.
This is the established contract value of the project as agreed by the organization, contracting parties, and other stakeholders. It becomes the baseline for monitoring the actual resources expended on the project.
At this stage, 30 to 70% of the project detail is completed. Most of the general project data and engineering deliverables are finalized. Drawings and datasheets of process units, equipment, and utilities are prepared for requesting vendor quotations.
Moreover, the project execution plans are starting to take shape. A thorough work breakdown structure (WBS), project timeline, equipment, and manpower scheduling, and material take-off are created.

The estimating method used now involves unit costs of line items instead of factoring methods seen from the previous estimate classes.
Aside from the technical specifications, a Class 2 estimate gives more focus to the project’s indirect costs. Overhead costs, contractors’ margins, administrative costs, and risk contingencies are some of the items included in the estimate’s line items.
The accuracy range for Class 2 estimates is -5 to -15% on the low side and +5 to +20% on the high side.
Class 1
Class 1 estimates are prepared for specific parts of the project. Subcontracting is the usual reason for calling a more detailed estimate.
This estimate forms a new baseline or control from which the bid of subcontractors is checked.
Another motive for creating Class 1 estimates is for controlling change or variation orders. Class 1 estimates are used for evaluating the claims of the contractor.
Typically, an established contract value comes first before the full definition of the project.

As the details are being completed, changes to the project scope arise. In turn, the fair price of the contract is altered. Class 1 estimates are accurate -3 to -10% on the low side, while +3 to +15% on the high side.
Other Classification Practices
Cost estimation practices can differ for each organization. These largely depend on their cost management policies and available capital.
Generally, a five-level system is used. However, some adopt a more streamlined system consisting of only three cost estimate categories.
The three categories are named based on how the estimates are used.
- Design estimates
- Bid estimates
- Control estimates
Design Estimates
Design estimates are prepared during the pre-design and detailed design phases of a project.
Throughout the engineering design, several estimates are typically prepared. These can either be categorized as Class 5, 4, or 3 estimates. The type depends on the project complexity and available information during the preparation of the estimate.
An initial design estimate is used to determine the feasibility of various construction methods. After that, another estimate is done from the schematic design. Finally, a more detailed estimate is made based on further developments to the design.
Following this templated approach can help determine a project’s initial cost assessment.
Bid Estimates
Bid estimates are prepared by contractors as part of the construction bidding process. Using several data inputs to prepare their estimates, construction contractors typically include:
- Quantities from material take-offs
- Subcontractor quotes
- Supervision costs
- Direct costs
Control Estimates
Control estimates are prepared before construction begins. They provide a baseline to assess and monitor construction costs as the project progresses.
The contractor may also use the control estimate for planning purposes to help keep the project budget on track.
Construction Cost Estimate Validation
As a system integrator with years of experience refining our digital workflows, we know how to make the most of a digital project executionDigital project execution (DPE) is a project management methodology that uses a data-centric approach to reduce project total-install-cost a… strategy. Whether it’s validating cost estimates or automating quality actions, Vista constantly collaborates with clients to implement new ways to shorten project schedules and reduce costs.
If you would like to learn more about how a digitally-enabled cost estimate validation process can help your project, contact Vista Projects today to schedule a consultation.
Cost Estimate Classes – FAQ
What are the three types of cost estimates?
Cost estimates can be classified into three types according to their intended purpose. The three types of cost estimates are design, bid, and control estimates.
Design estimates are prepared in the project preliminaries which gives the order of magnitude of the project cost. Bid estimates are used in the tendering phase of the project which details project overheads and other indirect costs.
Control estimates form the baseline of the project cost where the actual running costs are compared.
What are the four types of cost?
The four types of costs involved in a construction project are direct, indirect, fixed, and variable costs. Direct costs are costs related to the procurement of materials, equipment, and labor. They directly affect the project deliverables.
Indirect costs are attributed to expenses not associated directly with the project deliverables but are required for the smooth operation of the project. Examples are administrative costs, utilities, transportation, and other business overhead costs.
Fixed costs are expenses that are constant throughout the life cycle of the project. These are long-term costs such as the rental of major equipment and facilities.
Contrary to fixed costs are variable costs. These are costs that change depending on the stage of the project. An example is manpower salary. The number of personnel required varies according to the project’s current activity.
What is a high-level cost estimate?
A high-level cost estimate is a rough estimate used to initially pitch a project cost for budgetary purposes. They are considered in the middle of an order of magnitude estimate and a control estimate in terms of accuracy.
How do you estimate building costs?
Estimating building costs depends on the amount of current information at hand. In the early stages of the project, estimation is done by accounting for the amount of floor space of the building. This value is then multiplied by a factor or index based on historical data of past projects featuring similar outcomes.
After a considerable amount of design is conducted, the estimate can now be made more accurate by detailing the unit cost of line items. This estimate is more defined and does not rely on factoring methods.
What is a cost estimation review?
A cost estimation review is a process of checking the accuracy and reliability of a cost estimate. It ensures that the cost estimation basis, assumptions, and methodologies are properly accounted for. This process goes beyond the scope of the cost engineering team. Other groups such as engineering, project management, and project specialists are involved as well.